インダクタンスとリアクタンス ― コイルの特性（性質）と誘導性

コイルは、電気により磁界を生み出すことでさまざまな働きをします。その働きのもとになっているのが、インダクタンスとリアクタンスと呼ばれる作用・現象です。コイルが持つ特性と働き、インダクタンスとリアクタンスについてどのような関係があるのかを解説します。

コイルの特性と働き

コイルの働きを考えるうえで、切り離せない関係にあるのが電磁誘導とレンツの法則、そしてリアクタンスとインダクタンスです。

コイルは電線をらせん状に巻いた構造をしています。ここに電気を流したとき、電磁誘導により磁界が発生します。この電磁誘導が、コイルのさまざまな働きのもととなる現象です。

磁界と電流の間には、互いに変化を妨げる方向に働くという不思議な関係があります。電流が大きくなると逆向きの電流を発生させる方向に磁界が発生し、電流が小さくなるとそれを大きくする方向に磁界が発生します。また、電源から電流が供給されていない状態でも、磁界の変化を妨げる方向に電流が生じます。この電流と磁界の向きについての法則が、レンツの法則です。

このようにコイルは、流れる電流に変化があったとき、磁界の発生によってそれを妨げ、抵抗のように働きます。この働きをリアクタンスと呼び、その力の大きさをインダクタンスといいます。

コイルが起こす不思議な働きは、電磁誘導とレンツの法則、リアクタンスとインダクタンスによるものなのです。これらの原理から、コイルは電流の変化を吸収し安定させ、交流電流を通しにくく直流電流のみ通すという性質を持ちます。また、トランス（変圧器）が交流電圧の昇降を行う原理は、コイルの働きを応用したものです。

コイルとインダクタンス・リアクタンスに関する4つの法則

コイルが電磁誘導やレンツの法則、リアクタンスとインダクタンスによってさまざまな働きをするとき、そこにはいくつかの法則が成り立ちます。

自己誘導によるコイルのインダクタンス

コイルに流れる電流が変化したとき、コイルが発生させている磁界も変化します。この磁界の変化により電磁誘導が起こり、コイルに起電力が発生します。この現象を自己誘導と呼び、起電力と電流の変化率の間には次の関係が成り立ちます。

V：起電力［V］　L：インダクタンス［H］　ΔI/Δt：電流の変化率［A/t］

ソレノイドコイルのインダクタンス

インダクタンスはコイルの形状によって変わります。ここではソレノイドコイル（単層コイル）のインダクタンスについて考えてみましょう。ソレノイドコイルのインダクタンスは、次の式で表されます。

L：インダクタンス［H］　k：長岡係数　μ：透磁率［H/m］

N：コイルの巻き数　S：コイルの断面積［㎡］　l：コイル長［m］

自己誘導によるコイルの誘導起電力

電源とスイッチに、コイルと負荷（ランプ）が並列に接続された回路をつくったとき、スイッチをONにすると電流は緩やかに増大します。しかし、スイッチをOFFにしたときは瞬時に電流が小さくなるため、電流の変化率（ΔI/Δt）が大きくなり、もとの電源電圧より高い起電力が発生します。その結果、コイルと並列に接続されたランプは瞬間的により明るく点灯し、消灯します。この起電力によりランプが点灯している時間は、すでにスイッチはOFFになっているため電源からの電圧はかかっていません。コイルに電流が流れることで発生した磁界がエネルギーとして蓄えられ、それが瞬時に放出されるため大きな起電力が発生しているのです。このエネルギーには次のような関係が成り立ちます。

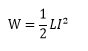
W：エネルギー［J］　L：インダクタンス［H］　I：電流［A］

このように起電力のエネルギーは、コイルのインダクタンスに比例し、電流の2乗に比例します。

交流に対するコイルの誘導性リアクタンス

コイルは電流の向きや大きさに変化があったとき、それを妨げるように磁界を発生させます。この作用から、直流電流はそのまま通しますが、交流電流に対しては抵抗のように働き、スムーズに通しません。この性質を、コイルの誘導性リアクタンスといいます。誘導性リアクタンスについての関係を表すのは次の式です。

  ：誘導性リアクタンス［Ω］　f：周波数［Hz］　L：インダクタンス［H］

このとき、誘導性リアクタンスを抵抗とみなすと、オームの法則により次の関係が成り立ちます。

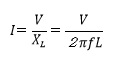
I：交流電流［A］　V：交流電圧［V］

コイル構造とインダクタンスの関係

コイルの構造や形状は、インダクタンスに大きく関係します。

ここでソレノイドコイルのインダクタンスを表す式をもう一度見てみましょう。

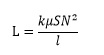
L：インダクタンス［H］　k：長岡係数　μ：透磁率［H/m］
N：コイルの巻き数　S：コイルの断面積［㎡］　l：コイル長［m］

インダクタンスの大きさはコアの透磁率とコイルの断面積に比例し、巻き数の2乗に比例しています。このことから、インダクタンスを大きくする条件として次のようなことが関係しているとわかります。

• コイル長が同じであれば断面積が大きいほどインダクタンスは大きくなる
• コアに使う物質の透磁率が高いほどインダクタンスは大きくなる
• 巻き数を増やせばインダクタンスは指数関数的に大きくなる

このような関係から考えると、大きなインダクタンスを得るためには単層巻きより多層巻きのほうが有効です。

しかし、コイルの巻き数を単純に増やした場合、巻いた層と層の間がコンデンサのように働き、電荷を蓄える性質を持つようになってしまいます。このため、余分な性質を除外する方法として工夫された巻き方が施されます。

例えば単層巻きの種類には次のような巻き方があります。

• 一層巻き
• スペース巻き

より大きなインダクタンスを得るために有効な多層巻きには、次のような種類があります。

• 整列巻き
• ランダム巻き
• ハニカム巻き
• バンク巻き
• バイファイラ巻き

また、インダクタンスを高くするためコアによく使われる透磁率の高い（＝磁化されやすい）物質は、次のようなものです。

• ケイ素鋼板
• パーマロイ
• パーミンバール
• フェライト
• 圧粉鉄心

電気と磁界によって不思議な働きをするコイル

コイルの性質と働き、それを表す代表的な4つの法則について紹介しました。

コイルは電気によって磁界をつくり、それによってより大きな電気を生み出す不思議な働きをします。その特性は、トランスや車のイグニッションなど、現代文明に必要不可欠な場面に深く浸透しています。コイルの働きに支えられて、人は電気をさまざまな用途で便利に使えているのです。

参考：

• コイルとは? ｜村田製作所
• コイルとは｜コトバンク
• コイルの種類と時定数を学ぶ 電子回路編｜APS
• インダクタ編　No.1「インダクタの基礎知識①」｜TDK株式会社
• インダクタ編　No.2「インダクタの基礎知識②」｜TDK株式会社

総合カタログ35
総合カタログ35は、IT業界・製造業で使用される当社製品をすべて網羅し、設計者、開閉装置（スイッチギア）メーカー、データセンター事業者のニーズを満たします。世界中で幅広く使用されている産業用キャビネット・ボックス、分電・配電システム、温度管理システム、ITインフラストラクチャ製品ラインアップの詳細情報を、936ページにわたってご紹介しています。

総合カタログ35　ダウンロード